pygimli.physics.petro#

Various petrophysical models

Overview#

Functions

`permeabilityEngelhardtPitter`(poro[, q, s, ...])	Empirical model for porosity to hydraulic permeability.
`resistivityArchie`(rFluid, porosity[, a, m, ...])	Resistivity of rock for the petrophysical model from Archies law.
`slownessWyllie`(phi[, sat, vm, vw, va, mesh, ...])	Return slowness \(s\) after Wyllie time-average equation.
`transFwdArchiePhi`([rFluid, m])	Archies law transformation function for resistivity(porosity).
`transFwdArchieS`([rFluid, phi, m, n])	Inverse Archie transformation function resistivity(saturation).
`transFwdWylliePhi`([sat, vm, vw, va])	Wyllie transformation function porosity(slowness).
`transFwdWyllieS`(phi[, vm, vw, va])	Wyllie transformation function slowness(saturation).
`transInvArchiePhi`([rFluid, m])	Inverse Archie transformation function porosity(resistivity).
`transInvArchieS`([rFluid, phi, m, n])	Inverse Archie transformation function saturation(resistivity).
`transInvWylliePhi`([sat, vm, vw, va])	Inverse Wyllie transformation function porosity(slowness).
`transInvWyllieS`(phi[, vm, vw, va])	Inverse Wyllie transformation function slowness(saturation).

Classes

`JointPetroInversion`(managers, trans[, ...])	TODO.
`PetroInversion`(manager, trans, **kwargs)	TODO.
`PetroJointModelling`([f, p, mesh, verbose])	Cumulative (joint) forward operator for petrophysical inversions.
`PetroModelling`(fop, trans[, mesh, verbose])	Combine petrophysical relation m(p) with modelling class f(p).

Functions#

pygimli.physics.petro.permeabilityEngelhardtPitter(poro, q=3.5, s=0.005, mesh=None, meshI=None)[source]#

Empirical model for porosity to hydraulic permeability.

Postulated for sand and sandstones. [v. Engelhardt and Pitter, 1955]

\[\begin{split}k & = 2\cdot 10^7 \frac{\phi^2}{(1-\phi)^2}* \frac{1}{S^2} \\ S & = q\cdot s \\ s & = \sum_{i=1}(\frac{P_i}{r_i})\end{split}\]

\(\phi\) - poro 0.0 –1.0
\(q\) - (3 for spheres, > 3 shape differ from sphere)
3.5 sand
\(s\) - in cm^-1 (s = 1/r for particles with homogeneous radii r)
\(P_i\) - Particle ration with radii \(r_i\) on 1cm^3 Sample
\(S\) - in cm^-1 specific surface in cm^2/cm^3

Returns:: in Darcy
Return type:: k

pygimli.physics.petro.resistivityArchie(rFluid, porosity, a=1.0, m=2.0, sat=1.0, n=2.0, mesh=None, meshI=None, fill=None, show=False)[source]#

Resistivity of rock for the petrophysical model from Archies law.

Calculates resistivity of rock for the petrophysical model from Archie’s law. [Archie, 1942]

\[\rho = a\rho_{\text{fl}}\phi^{-m} S^{-n}\]

\(\rho\) - the electrical resistivity of the fluid saturated rock in \(\Omega\text{m}\)
\(\rho_{\text{fl}}\) - rFluid: electrical resistivity of the fluid in \(\Omega\text{m}\)
\(\phi\) - porosity 0.0 –1.0
\(S\) - fluid saturation 0.0 –1.0 [sat]
\(a\) - Tortuosity factor. (common 1)
\(m\) - Cementation exponent of the rock (usually in the range 1.3 – 2.5 for sandstones)
\(n\) - is the saturation exponent (usually close to 2)

If mesh is not None the resulting values are calculated for each cell of the mesh. All parameter can be scalar, array of length mesh.cellCount() or callable(pg.cell). If rFluid is non-steady n-step distribution than rFluid can be a matrix of size(n, mesh.cellCount()) If meshI is not None the result is interpolated to meshI.cellCenters() and prolonged (if fill ==1).

Notes

We experience some unstable nonlinear behavior. Until this is clarified all results are rounded to the precision 1e-6.

Examples

>>> #

WRITEME

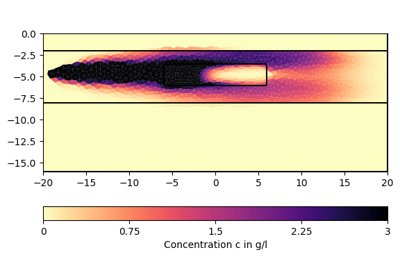
Examples using pygimli.physics.petro.resistivityArchie

Hydrogeophysical modelling

pygimli.physics.petro.slownessWyllie(phi, sat=1, vm=4000, vw=1484, va=343, mesh=None, meshI=None, fill=None)[source]#

Return slowness \(s\) after Wyllie time-average equation.

\[s = (1-\phi) \cdot\frac{1}{v_m} + \phi \cdot S \cdot\frac{1}{v_w} + \phi \cdot(1 - S) \cdot\frac{1}{v_a}\]

\(\phi\) - porosity 0.0 –1.0
\(S\) - fluid saturation 0.0 –1.0 [sat]
\(v_m\) - velocity of matrix [4000 m/s]
\(v_w\) - velocity of water [1484 m/s]
\(v_a\) - velocity of air [343 m/s]

If mesh is not None the resulting values are calculated for each cell of the mesh. All parameter can be scalar, array of length mesh.cellCount() or callable(pg.cell). If meshI is not None the result is interpolated to meshI.cellCenters() and prolonged (if fill ==1).

Examples

WRITEME

pygimli.physics.petro.transFwdArchiePhi(rFluid=20, m=2)[source]#

Archies law transformation function for resistivity(porosity).

\[\begin{split}\rho & = a\rho_{\text{fl}}\phi^{-m}\S_w^{-n} \\ \rho & = \rho_{\text{fl}}\phi^(-m) = \left(\phi/\rho_{\text{fl}}^{-1/n}\right)^{-n}\end{split}\]

Returns:: trans – Transformation function
Return type:: GIMLI::RTransPower

Examples

>>> from pygimli.physics.petro import *
>>> phi = 0.3
>>> tFAPhi = transFwdArchiePhi(rFluid=20)
>>> r1 = tFAPhi.trans(phi)
>>> r2 = resistivityArchie(rFluid=20.0, porosity=phi,
...                        a=1.0, m=2.0, sat=1.0, n=2.0)
>>> print(r1-r2 < 1e-12)
True
>>> phi = [0.3]
>>> tFAPhi = transFwdArchiePhi(rFluid=20)
>>> r1 = tFAPhi.trans(phi)
>>> r2 = resistivityArchie(rFluid=20.0, porosity=phi,
...                        a=1.0, m=2.0, sat=1.0, n=2.0)
>>> print((r1-r2 < 1e-12)[0])
True

pygimli.physics.petro.transFwdArchieS(rFluid=20, phi=0.4, m=2, n=2)[source]#: Inverse Archie transformation function resistivity(saturation).

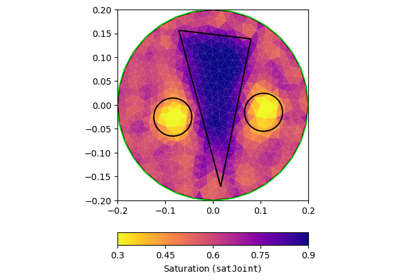
Examples using pygimli.physics.petro.transFwdArchieS

Petrophysical joint inversion

pygimli.physics.petro.transFwdWylliePhi(sat=1, vm=4000, vw=1600, va=330)[source]#: Wyllie transformation function porosity(slowness).

pygimli.physics.petro.transFwdWyllieS(phi, vm=4000, vw=1600, va=330)[source]#: Wyllie transformation function slowness(saturation).

Examples using pygimli.physics.petro.transFwdWyllieS

Petrophysical joint inversion

pygimli.physics.petro.transInvArchiePhi(rFluid=20, m=2)[source]#

Inverse Archie transformation function porosity(resistivity).

# rFluid/rho = phi^m ==> phi = (rFluid/rho)^(1/m) = (rho/rFluid)^(-1/m) See — pygimli.physics.petro.transFwdArchiePhi

pygimli.physics.petro.transInvArchieS(rFluid=20, phi=0.4, m=2, n=2)[source]#: Inverse Archie transformation function saturation(resistivity).

pygimli.physics.petro.transInvWylliePhi(sat=1, vm=4000, vw=1600, va=330)[source]#: Inverse Wyllie transformation function porosity(slowness).

pygimli.physics.petro.transInvWyllieS(phi, vm=4000, vw=1600, va=330)[source]#: Inverse Wyllie transformation function slowness(saturation).

Classes#

class pygimli.physics.petro.JointPetroInversion(managers, trans, verbose=False, debug=False, **kwargs)[source]#

Bases: MethodManager

TODO.

__init__(managers, trans, verbose=False, debug=False, **kwargs)[source]#: TODO.

static createFOP(verbose=False)[source]#: Create forward operator.

createInv(fop, verbose=True, doSave=False)[source]#: TODO.

invert(data=None, mesh=None, lam=20, limits=None, **kwargs)[source]#: TODO.

model()[source]#: Inversion model.

setData(data)[source]#: TODO.

setMesh(mesh)[source]#: TODO.

showModel(**showkwargs)[source]#: TODO.

class pygimli.physics.petro.PetroInversion(manager, trans, **kwargs)[source]#

Bases: JointPetroInversion

TODO.

__init__(manager, trans, **kwargs)[source]#: TODO.

invert(data, **kwargs)[source]#: TODO.

class pygimli.physics.petro.PetroJointModelling(f=None, p=None, mesh=None, verbose=True)[source]#

Bases: Modelling

Cumulative (joint) forward operator for petrophysical inversions.

__init__(f=None, p=None, mesh=None, verbose=True)[source]#: Constructor.

createJacobian(model)[source]#: Creating individual Jacobian matrices.

initJacobian()[source]#: TODO.

response(model)[source]#: Create concatenated response for fop stack with model.

setData(data)[source]#: TODO.

setFopsAndTrans(fops, trans)[source]#: TODO.

setMesh(mesh)[source]#: TODO.

class pygimli.physics.petro.PetroModelling(fop, trans, mesh=None, verbose=False)[source]#

Bases: Modelling

Combine petrophysical relation m(p) with modelling class f(p).

Combine petrophysical relation m(p) with modelling class f(p) to invert for m (or any inversion transformation) instead of p.

__init__(fop, trans, mesh=None, verbose=False)[source]#: Save forward class and transformation, create Jacobian matrix.

createJacobian(model)[source]#: Fill the individual jacobian matrices.

response(model)[source]#: Use inverse transformation to get p(m) and compute response.

setData(data)[source]#: TODO.

setMesh(mesh)[source]#: TODO.