Heat equation in 2D

This tutorial solves the stationary heat equation in 2D. The example is taken from the pyGIMLi paper (https://cg17.pygimli.org).

import pygimli as pg
import pygimli.meshtools as mt

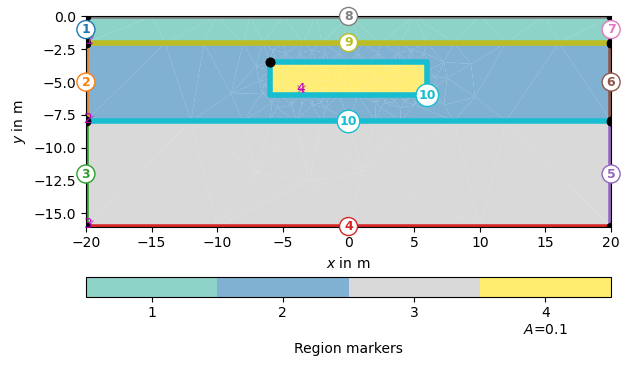
Create geometry definition for the modelling domain.

world = mt.createWorld(start=[-20, 0], end=[20, -16], layers=[-2, -8],
                       worldMarker=False)
# Create a heterogeneous block
block = mt.createRectangle(start=[-6, -3.5], end=[6, -6.0],
                           marker=4,  boundaryMarker=10, area=0.1)
# Merge geometrical entities
geom = world + block
ax, cb = pg.show(geom, markers=True)

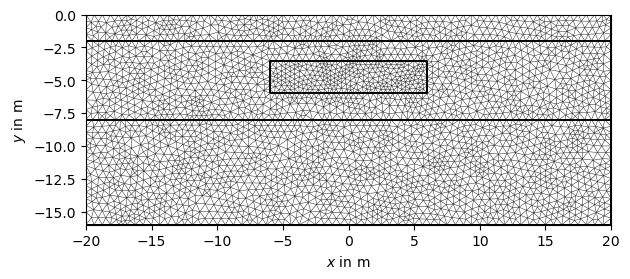
Create a mesh from based on the geometry definition. When calling the pg.meshtools.createMesh() function, a quality parameter can be forwarded to Triangle, which prescribes the minimum angle allowed in the final mesh. For a tutorial on the quality of the mesh please refer to : Mesh quality inspection [1] [1]: https://www.pygimli.org/_tutorials_auto/1_basics/plot_6-mesh-quality-inspection.html#sphx-glr-tutorials-auto-1-basics-plot-6-mesh-quality-inspection-py Note: Incrementing quality increases computer time, take precaution with quality values over 33.

mesh = mt.createMesh(geom, quality=33, area=0.2, smooth=[1, 10])
ax, _ = pg.show(mesh)

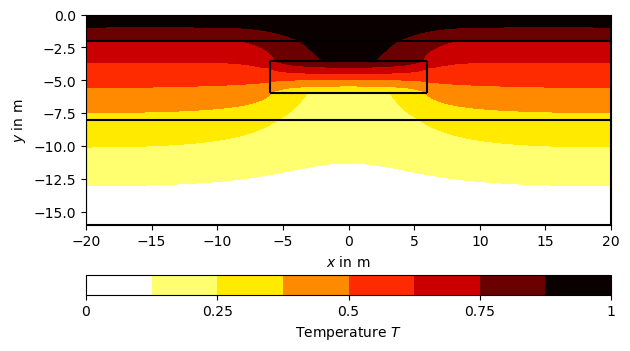
Call pygimli.solver.solveFiniteElements() to solve the heat diffusion equation \(\nabla\cdot(a\nabla T)=0\) with \(T(bottom)=0\) (boundary marker 8) and \(T(top)=1\) (boundary marker 4), where \(a\) is the thermal diffusivity and \(T\) is the temperature distribution. We assign thermal diffusivities to the four # regions using their marker numbers in a dictionary (a) and the fixed temperatures at the boundaries using Dirichlet boundary conditions with the respective markers in another dictionary (bc)

T = pg.solver.solveFiniteElements(mesh,
                                  a={1: 1.0, 2: 2.0, 3: 3.0, 4:0.1},
                                  bc={'Dirichlet': {8: 1.0, 4: 0.0}}, verbose=True)
ax, _ = pg.show(mesh, data=T, label='Temperature $T$',
                cMap="hot_r", nCols=8, contourLines=False)

ax, _ = pg.show(geom, ax=ax, fillRegion=False)

Mesh:  Mesh: Nodes: 3011 Cells: 5832 Boundaries: 8842
Assembling time:  0.049893468
Solving time:  0.013399571