Note
Go to the end to download the full example code.
Matrices#
There is a large number of Matrix types that are all derived from the
base class MatrixBase. They do not have to store elements but can be
logical or wrappers. They just have to provide the functions
A.cols(), A.rows() (column and row numbers),
A.mult(x)\(=A\cdot x\) and A.transMult(y)\(=A^T\cdot y\).
# We start off with the typical imports
import numpy as np
import pygimli as pg
Dense matrix Matrix#
All elements are stored column-wise, i.e. all rows A[i] are of type
pg.Vector. This matrix is used for storing dense data (like ERT
Jacobians) and doing simple algebra.
RMatrix: 3 x 4
4 [1.0, 0.0, 0.0, 0.0]
4 [0.0, 1.0, 2.0, 3.0]
4 [0.0, 0.0, -1.0, 0.0]
3 [5.0, 44.0, -7.0]
Exists also as complex matrix under pg.matrix.CMatrix.
Index-based sparse matrix SparseMapMatrix#
Sparse matrix (most elements are zero) with single access and. Typical for traveltime Jacobian (only certain cells covered by individual rays) or constraint matrices.
2 [2.0, 1.0]
Exists also as complex-valued variant pg.matrix.CSparseMapMatrix.
Column-compressed matrix SparseMatrix#
Used for numerical approximation of partial differential equations like
finite-element or finite volume. Not typically used unless efficiency is
of importance. It exists also complex-valued as pg.matrix.CSparseMatrix.
Diagonal matrices#
First, there is an identity matrix IdentityMatrix. No elements
stored at all. Important for constraint matrices when combined into
BlockMatrix (see below). More generally, there is a diagonal matrix
DiagonalMatrix where only its diagonal is stored as vector.
3 [10.0, 11.0, 12.0]
Weighted matrices#
MultLeftMatrix/MultRightMatrix/MultLeftRightMatrix
Often, matrices are weighted from either side by a vector, e.g. data error weighting of the Jacobian matrix, data and model transformations, or weighting individual smoothness parts according to the roughness so that only the weighting is changed and not the matrix.
3 [6.0, 6.0, 6.0]
3 [12.0, 18.0, -6.0]
Combinations of matrices#
Logical matrices can combine different other matrices (of arbitrary
type) avoiding double memory storage by multiplication (Mult2Matrix)
or addition (Add2Matrix).
2 [0.0, 0.0]
Block matrices#
The most important type is the BlockMatrix, where arbitrary matrices
are combined into a logical matrix. This is of importance for inversion
frameworks: * joint inversion: Jacobian matrices are concatenated *
combination of different constrains: combining different regularization
* laterally, spatially or temporally constrained inversion:
regularization between model cells of each frame but also between the
frames Note that the matrices only have to be defined once and can
appear multiply.
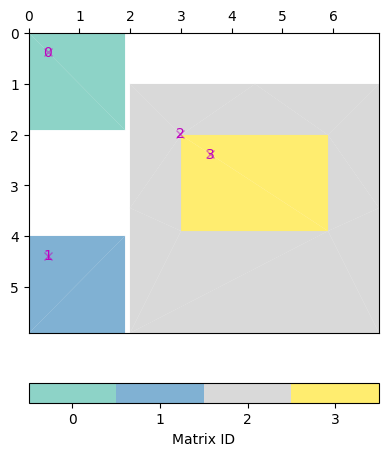
pg.matrix.BlockMatrix of size 6 x 7 consisting of 4 submatrices.
Matrix combinations#
There are also simpler types of matrix combinations: *
H2Matrix/V2Matrix: two matrices below/next to each other *
HNMatrix/VNMatrix: one matrix repeated N times
horizontally/vertically * NDMatrix: block diagonal matrix
Matrix wrappers#
TransposedMatrix avoids transposing any matrix by exchanging left/right mult. SquaredMatrix keeps only the matrix A but works as A^T @ A SquaredTransposeMatrix keeps only the matrix A but works as A @ A.T RealNumpyMatrix holds a real-valued numpy array ComplexNumpyMatrix holds a complex-valued numpy array in a real pg matrix NumpyMatrix
Matrix generators#
Often, several matrices or even the same one have to be combined. RepeatHMatrix, RepeatVMatrix, RepeatDMatrix hold a single matrix that is repeated horizontally, vertically or diagonally. NDMatrix, FrameConstraintMatrix is a special generator for constraining cells of every (e.g. timelapse) frame and moreover the frames with each other.
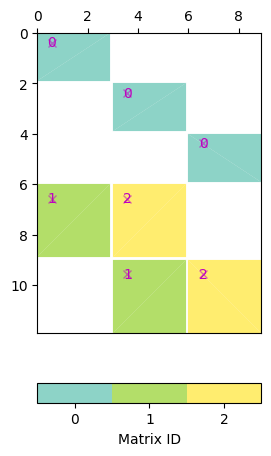
pg.matrix.BlockMatrix of size 12 x 9 consisting of 7 submatrices.
Geostatistical constraint matrix#
For geostatistical constraints, a correlation matrix is computed using correlation lengths and angles to define their directions. To access its inverse root in a way that avoids matrix inversion, an eigenvalue decomposition is done and the eigenvalues \(D`\) and -vectors \(Q\) are stored so that the operator
Jordi, C., Doetsch, J., Günther, T., Schmelzbach, C. & Robertsson, J.O.A. (2018): Geostatistical regularisation operators for geophysical inverse problems on irregular meshes. Geophysical Journal International 213, 1374- 1386, doi:10.1093/gji/ggy055.