Gravimetry in 2D - Part I

Simple gravimetric field solution.

Calculate for the gravimetric potential \(u\)

\[\frac{\partial u}{\partial z}\]

along a profile for a cylindrical heterogeneity with different approaches.

import numpy as np
import pygimli as pg
from pygimli.meshtools import createCircle, createWorld, createMesh

from pygimli.physics.gravimetry import gradUCylinderHoriz, solveGravimetry

radius = 2.  # [m]
depth = 5.  # [m]
pos = [0., -depth]
dRho = 100

x = np.arange(-20, 20.1, .5)
pnts = np.array([x, np.zeros(len(x))]).T

Analytical solution first

gz_a = gradUCylinderHoriz(pnts, radius, dRho, pos)[:, 1]

Integration for a 2D polygon after [Won and Bevis, 1987]

circ = createCircle([0, -depth], radius=radius, marker=2, area=0.1,
                    nSegments=16)
gz_p = solveGravimetry(circ, dRho, pnts, complete=False)

Integration for complete 2D mesh after [Won and Bevis, 1987]

world = createWorld(start=[-20, -10], end=[20, 0], marker=1)
mesh = createMesh([world, circ])
dRhoC = pg.solver.parseMapToCellArray([[1, 0.0], [2, dRho]], mesh)
gc_m = solveGravimetry(mesh, dRhoC, pnts)

Finite Element solution for \(u\)

world = createWorld(start=[-200, -200], end=[200, 200], marker=1)

# Add some nodes to the measurement points to increase the accuracy a bit
[world.createNode(x_, 0.0,  1) for x_ in x]
plc = world + circ
mesh = createMesh(plc, quality=34)
mesh = mesh.createP2()

density = pg.solver.parseMapToCellArray([[1, 0.0], [2, dRho]], mesh)
u = pg.solver.solve(mesh, a=1, f=density, bc={'Dirichlet': {-2: 0, -1: 0}})

Calculate gradient of gravimetric potential \(\frac{\partial u}{\partial (x,z)}\)

dudz = np.zeros(len(pnts))

for i, p in enumerate(pnts):
    c = mesh.findCell(p)
    g = c.grad(p, u)
    dudz[i] = -g[1] * 4. * np.pi * pg.physics.constants.GmGal  # why 4 pi here?

Finishing the plots

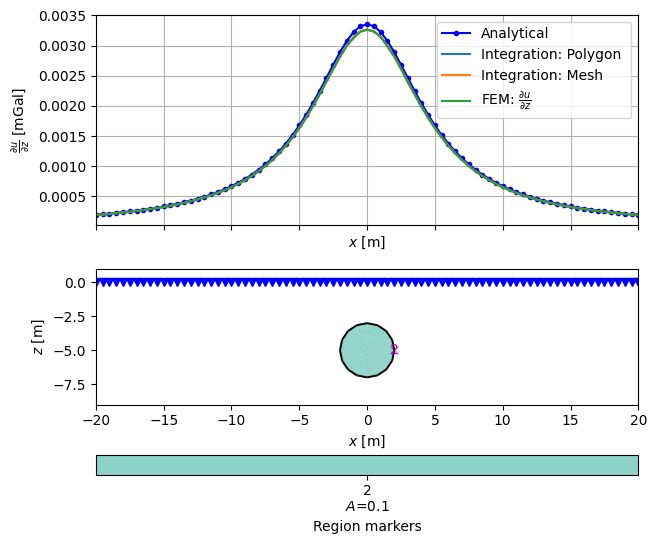
fig, (ax1, ax2) = pg.plt.subplots(2, 1, sharex=True, figsize=(7, 6))
ax1.plot(x, gz_a, '-b', marker='.', label='Analytical')
ax1.plot(x, gz_p, label='Integration: Polygon ')
ax1.plot(x, gc_m, label='Integration: Mesh')
ax1.plot(x, dudz, label=r'FEM: $\frac{\partial u}{\partial z}$')

pg.show(circ, ax=ax2)
ax2.plot(x, x*0, 'bv')

ax1.set_ylabel(r'$\frac{\partial u}{\partial z}$ [mGal]')
ax1.set_xlabel('$x$ [m]')
ax1.grid()
ax1.legend()

ax2.set_aspect(1)
ax2.set_xlabel('$x$ [m]')
ax2.set_ylabel('$z$ [m]')
ax2.set_ylim((-9, 1))
ax2.set_xlim((-20, 20))

pg.wait()