6. Modelling#

6.1. Theory (Finite Element Analysis)#

This tutorial covers the first steps into Finite Element computation referring the M (Modelling) in pyGIMLi.

We will not dig into deep details about the theory of the Finite Elements Analysis (FEA) here, as this can be found in several books, e.g., [Zienkiewicz, 1977].

Anyhow, there is a little need for theory to understand what it means to use FEA for the solution of a boundary value problem. So we start with some basics.

Assuming Poisson’s equation as a simple partial differential problem to be solved for the sought scalar field \( u(\mathbf{r}) \) within a modelling domain \({r}\in\Omega`\) with a non-zero right-hand side function \( f \).

\[\begin{split} - \Delta u = f \quad{\mathrm{in}}\quad~\Omega \\ u = g \quad{\mathrm{on}}\quad\partial\Omega\ \end{split}\]

The Laplace operator \( `\Delta = \nabla\cdot\nabla` \) given by the divergence of the gradient, is the sum of the second partial derivatives of the field \(`u(\mathbf{r})`\) with respect to the Cartesian coordinates in 1D space \( \mathbf{r} = (x) \), in 2D \( {r} = (x, y) \), or 3D space \( \mathbf{r} = (x, y, z) \). On the boundary \( \partial\Omega \) of the domain, we want known values of \( u=g \) as so called Dirichlet boundary conditions.

A common approach to solve this problem is the method of weighted residuals. The base assumption states that an approximated solution \( u_h\approx u\) will only satisfy the differential equation with a rest \( R \) : \(\Delta u_h + f = R \). If we choose some weighting functions \( w \), we can try to minimize the resulting residuum over our modelling domain as:

\[ \int_{\Omega} R w = 0\; \]

which leads to:

\[ \int_{\Omega} - \Delta u_h w = \int_{\Omega} f w\ \]

It is preferable to eliminate the second derivative in the Laplace operator, either due to integration by parts or by applying the product rule and Gauss’s law. This leads to the so called weak formulation:

\[ \int_{\Omega} \nabla u_h \nabla w - \int_{\partial \Omega}\mathbf{n}\nabla u_h w = \int_{\Omega} f w \]
\[ \int_{\Omega} \nabla u_h \nabla w = \int_{\Omega} f w + \int_{\partial \Omega}\frac{\partial u_h}{\partial\mathbf{n}} w\ \]

We can solve these integrals after choosing an appropriate basis for an approximate solution \( u_h \) as:

\[ u_h = \sum_i \mathrm{u}_i N_i\quad\text{with}\quad i = 0\ldots\mathcal{N}\ \]

The latter fundamental FEA relation discretizes the continuous solution \( u_h \) into a discrete values \( \mathrm{u} = \{\mathrm{u}_i\} \) for a number of \( i = 0\ldots\mathcal{N} \) discrete points, usually called nodes.

The basis functions \( N_i \) can be understood as interpolation rules for the discrete solution between adjacent nodes and will be chosen later.

Now we can set the unknown weighting functions to be the same as the basis functions \( w=N_j \) with \( j=0\ldots\mathcal{N} \) (Galerkin method)

\[ \int_{\Omega} \sum_i \mathrm{u}_i \nabla N_i \nabla N_j = \int_{\Omega} f_j N_j + \int_{\partial \Omega} h N_j \quad \text{with}\quad h = \frac{\partial u}{\partial \mathbf{n}} \]

this can be rewritten with \(h=0\) as:

\[ \mathrm{A} \mathrm{u} = \mathrm{b} \]
\[ \text{with } \mathrm{A} = \{\mathrm{a}_{i,j}\} = \int_{\Omega}\nabla N_i \nabla N_j \quad\text{known as 'Stiffness matrix'} \]
\[ \mathrm{b} = \{\mathrm{b}_j\} = \int_{\Omega} f_j N_j \quad\text{known as 'Load vector'} \]

The solution of this linear system of equations leads to the discrete solution \( \mathrm{u} = \{\mathrm{u}_i\} \) for all \( i=1\ldots\mathcal{N}`\) nodes inside the modelling domain.

For the practical part, the choice of the nodes is crucial. If we choose too little, the accuracy of the sought solution might be too small. If we choose too many, the dimension of the system matrix will be too large, which leads to higher memory consumption and calculation times.

To define the nodes, we discretize our modelling domain into cells, or the eponymous elements. Cells are basic geometric shapes like triangles or hexahedrons and are constructed from the nodes and collected in a mesh. For more details, refer to the Meshes section of the user guide. In summary, the discrete solutions of the differential equation using FEA on a specific mesh are defined on the node positions of the mesh.

To complete the solution for the small example, we still need to apply the boundary condition \(u=g\) which is known as the Dirichlet condition. Setting explicit values for our solution is not covered by the general Galerkin weighted residuum method but we can solve it algebraically. We reduce the linear system of equations by the known solutions \(g={g_k}\) for all \(k\) nodes on the affected boundary elements:

\[\begin{split} \mathrm{A_D}\cdot\mathrm{u} = \mathrm{b_D} \\ \text{with } \mathrm{A_D} = \{\mathrm{a}_{i,j}\}\quad\forall i, j ~\notin~ k ~\text{and}~1~\text{for}~i,j \in k\\ \mathrm{b_D} = \{\mathrm{b}_j\} - \mathrm{A}\cdot\mathrm{g}\quad\forall j \notin k~\text{and}~g_k~\text{for}~j \in k \end{split}\]

Now we have all parts together to assemble \(\mathrm{A_D}\) and \(\mathrm{b_D}\) and finally solve the given boundary value problem.

It is usually a good idea to test a numerical approach with known solutions. To keep things simple we create a modelling problem from the reverse direction. We choose a solution, calculate the right hand side function and select the domain geometry suitable for nice Dirichlet values.

\[ u(x,y) = \operatorname{sin}(x)\operatorname{sin}(y) \]
\[ - \Delta u = f(x,y) = 2 \operatorname{sin}(x)\operatorname{sin}(y) \]
\[ \Omega \in I\!R^2 \quad \text{on}\quad 0 \leq x \leq 2\pi,~~ 0 \leq y \leq 2\pi \]
\[ u = g = 0 \quad \text{on}\quad \partial \Omega \]

We now can solve the Poison equation applying the FEA capabilities of pygimli and compare the resulting approximate solution \(\mathrm{u}\) with our known exact solution \(u(x,y)\).

6.2. Parameterizing a mesh with physical properties#

Hide code cell content 
import numpy as np
import pygimli as pg

from pygimli.solver import solve
from pygimli.viewer import show
from pygimli.viewer.mpl import drawStreams
import pygimli.meshtools as mt

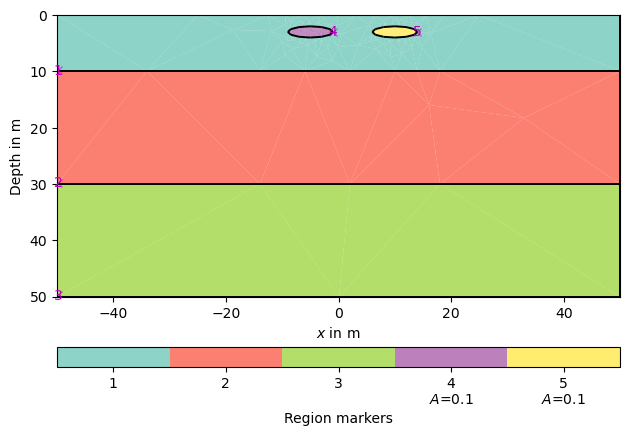
We can parametrize a mesh that has been made with different physical properties depending on the region. For example, we have the following polygons created as PLC and created a mesh from this:

Create geometry definition for the modelling domain. worldMarker=True indicates the default boundary conditions for the ERT. Here we are also creating layers at y=-10 and y=-30. This will make a world with 3 different markers for the 3 distinct layers.

world = mt.createWorld(start=[-50, 0], end=[50, -50], layers=[-10, -30],worldMarker=True)

Create some heterogeneous circular anomaly and assign the following markers:

block_1 = mt.createCircle(pos=[-5, -3.], radius=[4, 1], marker=4,
                        boundaryMarker=10, area=0.1)
block_2  = mt.createCircle(pos=[10, -3.], radius=[4, 1], marker=5,
                        boundaryMarker=10, area=0.1)

Merge geometry definition into a Piecewise Linear Complex (PLC) and plot it using pg.show, you can pass markers=True to get a look at how your regions are numbered. Also, you can set boundaryMarkers=True to analyze the boundary markers which will be explained in the next section.

geom = world + block_1 + block_2
pg.show(geom, markers=True, boundaryMarkers=False)

(<AxesSubplot: xlabel='$x$ in m', ylabel='Depth in m'>, None)
../../_images/fcfac0889f4c97469e78d2c6a82eefa53c70dfd384f82990d2a2e3a38d2968a4.png

Create a mesh for the finite element modelling with appropriate mesh quality.

mesh = mt.createMesh(geom, quality=34)

You can also print the amount of markers that are in the mesh by using the following commands:

number_of_cellmarkers = list(set(mesh.cellMarkers()))
print(number_of_cellmarkers)

[1, 2, 3, 4, 5]

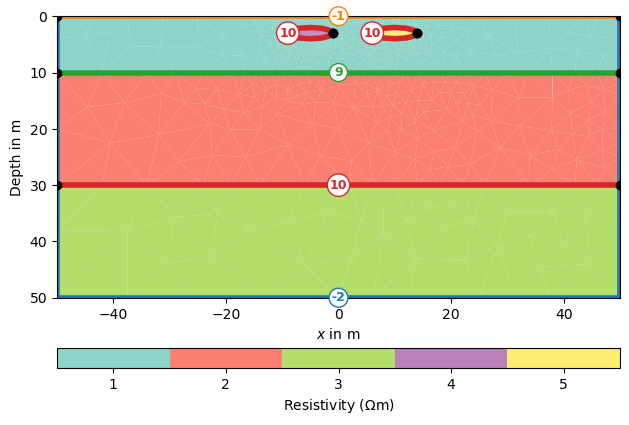
Create a map to set resistivity values in the appropriate regions [[regionNumber, resistivity], [regionNumber, resistivity], […]

rhomap = [[1, 100.],
          [2, 75.],
          [3, 50.],
          [4, 150.],
          [5, 25]]

Here we assigned a different resistivity value to each part of the mesh using its cell markers and we can view the resistivity distribution with the following command:

pg.show(mesh, data=rhomap, label=pg.unit('res'), markers=True)

(<AxesSubplot: xlabel='$x$ in m', ylabel='Depth in m'>,
 <matplotlib.colorbar.Colorbar at 0x1482d73fad90>)
../../_images/bc6cc78b2a1dd6588c5bd374ca5b71801786d6123fb58e82e609a1de18a66f44.png

We will now show the different options to set boundary conditions and get these ready to then simulate and model the data.

6.3. Boundary conditions (BC)#

Definition of Boundary Conditions

  • Boundary marker (-1) : surface boundary conditions - pg.core.MARKER_BOUND_HOMOGEN_NEUMANN

  • Boundary marker (-2) : mixed-boundary conditions - pg.core.MARKER_BOUND_MIXED

  • Boundary marker ( >= 1 ) : no-flow boundaries

As shown in meshes section of the user guide, pyGIMLi automatically assigns boundaries when using mt.createWorld(). However, you can assign BCs to different elements of your PLC or mesh.

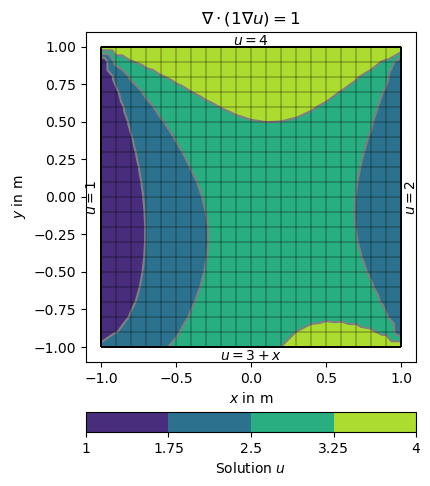
There are different ways of specifying BCs. They can be maps from markers to values, explicit functions or implicit (lambda) functions. We use the example of the Poisson equation on the unit square and specify different boundary conditions on the four sides.

  • The boundary 1 (left) and 2 (right) are directly mapped to the values 1 and 2.

  • On side 3 (top) a lambda function 3+x is used (p is the boundary position and p[0] its x coordinate).

  • On side 4 (bottom) a function uDirichlet is used that simply returns 4 in this example but can compute anything as a function of the individual boundaries b.

def uDirichlet(boundary):
    """Return a solution value for a given boundary.
        Scalar values are applied to all nodes of the boundary."""
    return 4.0

dirichletBC = {1: 1,                                           # left
               2: 2.0,                                         # right
               3: lambda boundary: 3.0 + boundary.center()[0], # bottom
               4: uDirichlet}                                  # top

The boundary conditions are passed using the BC keyword dictionary dirichletBC.

grid = pg.createGrid(x=np.linspace(-1.0, 1.0, 21),
                     y=np.linspace(-1.0, 1.0, 21))
u = solve(grid, f=1., bc={'Dirichlet': dirichletBC})

# Note that showMesh returns the created figure ax and the created colorBar.
ax, cbar = show(grid, data=u, label='Solution $u$')

show(grid, ax=ax)

ax.text(1.02, 0, '$u=2$', va='center', ha='left',  rotation='vertical')
ax.text(-1.01, 0, '$u=1$', va='center', ha='right', rotation='vertical')
ax.text(0, 1.01, '$u=4$', ha='center')
ax.text(0, -1.01, '$u=3+x$', ha='center', va='top')

ax.set_title('$\\nabla\cdot(1\\nabla u)=1$')

ax.set_xlim([-1.1, 1.1])  # some boundary for the text
ax.set_ylim([-1.1, 1.1])

(-1.1, 1.1)
../../_images/3e99d5ceda6616ce5163c893d2670140bb1fafddd67dff3057e74e9db2f24006.png

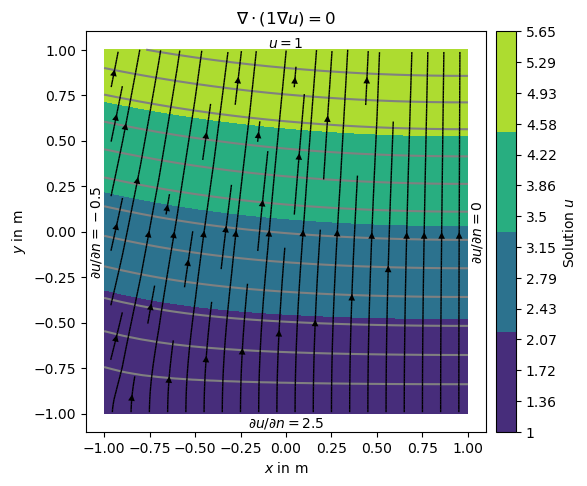
Alternatively we can define the gradients of the solution on the boundary, i.e., Neumann type BC. This is done with another dictionary {marker: value} and passed by the bc dictionary.

neumannBC = {1: -0.5,  # left
             4: 2.5}  # bottom

dirichletBC = {3: 1.0}  # top

u = solve(grid, f=0., bc={'Dirichlet': dirichletBC, 'Neumann': neumannBC})

Note that on boundary 2 (right) has no BC explicitly applied leading to default (natural) BC that are of homogeneous Neumann type \(\frac{\partial u}{\partial n}=0\)

ax = show(grid, data=u, filled=True, orientation='vertical',
          label='Solution $u$',
          levels=np.linspace(min(u), max(u), 14), hold=True)[0]

# Instead of the grid we now want to add streamlines to show the gradients of
# the solution (i.e., the flow direction).
drawStreams(ax, grid, u)
ax.text(0.0, 1.01, '$u=1$',
        horizontalalignment='center')  # top -- 3
ax.text(-1.0, 0.0, '$\partial u/\partial n=-0.5$',
        va='center', ha='right', rotation='vertical')  # left -- 1
ax.text(0.0, -1.01, '$\partial u/\partial n=2.5$',
        ha='center', va='top')  # bot -- 4
ax.text(1.01, 0.0, '$\partial u/\partial n=0$',
        va='center', ha='left', rotation='vertical')  # right -- 2

ax.set_title('$\\nabla\cdot(1\\nabla u)=0$')

ax.set_xlim([-1.1, 1.1])
ax.set_ylim([-1.1, 1.1])

(-1.1, 1.1)
../../_images/e084c8638c606b062099075ba5f417053c35a1e09300c12c15cc3e40a9252726.png

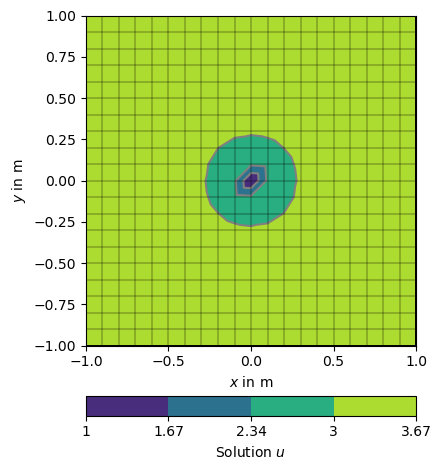
Its also possible to force single nodes to fixed values too.

u = solve(grid, f=1., bc={'Node': [grid.findNearestNode([0.0, 0.0]), 1.0]})
np.testing.assert_approx_equal(u[grid.findNearestNode([0.0, 0.0])], 1.0, significant=10)

ax, _ = pg.show(grid, u, logScale=False, label='Solution $u$',)
_ = pg.show(grid, ax=ax)
../../_images/0c55d1c9650d44068d95f319b6327d63bf009f4f8443fa1d5f48deca8c520fc0.png