# Checkout www.pygimli.org for more examples

3D gravity modelling and inversion#

Based on the synthetic model of Li & Oldenburg (1998), we demonstrate 3D inversion of magnetic data. The forward operator bases on the formula given by Holstein et al. (2007).

In the following, we will build the model, create synthetic data, and do inversion using a depth-weighting function as outlined in the paper.

import numpy as np
import matplotlib.pyplot as plt
import pygimli as pg
from pygimli.viewer import pv
from pygimli.physics.gravimetry import GravityModelling

Synthetic model and data generation#

The grid is 1x1x0.5 km with a spacing of 50 m.

dx = 50
x = np.arange(0., 1001, dx)
y = np.arange(0., 1001, dx)
z = np.arange(0., 501, dx)
grid = pg.createGrid(x, y, z)
print(grid)

We create a 3D matrix that is later filled as vector into the grid. The model consists of zeros and patches of 5x6 cells per depth slice that are shifted by one cell for subsequent cells.

v = np.zeros((len(z)-1, len(y)-1, len(x)-1))
for i in range(7):
    v[1+i, 11-i:16-i, 7:13] = 1 # 1g/cm³

grid["synth"] = v.ravel()

We show the model making use of the pyvista package that can be called by :py:func:pygimli.show. The mesh itself is shown as a wireframe, the anomaly is plotted as a surface plot using a threshold filter. After the first call with hold=True, the plotter is used to draw any subsequent plots that can also be slices or clips. Moreover, the camera position is set so that the vertical axis is going downwards (x is Northing and y is Easting as common in magnetics).

pl, _ = pg.show(grid, style="wireframe", hold=True)
pv.drawMesh(pl, grid, label="synth", style="surface", cMap="Spectral_r",
            filter={"threshold": dict(value=0.05, scalars="synth")})
pl.camera_position = "yz"
pl.camera.roll = 90
pl.camera.azimuth = 180 - 15
pl.camera.elevation = 10
pl.camera.zoom(1.2)
_ = pl.show()

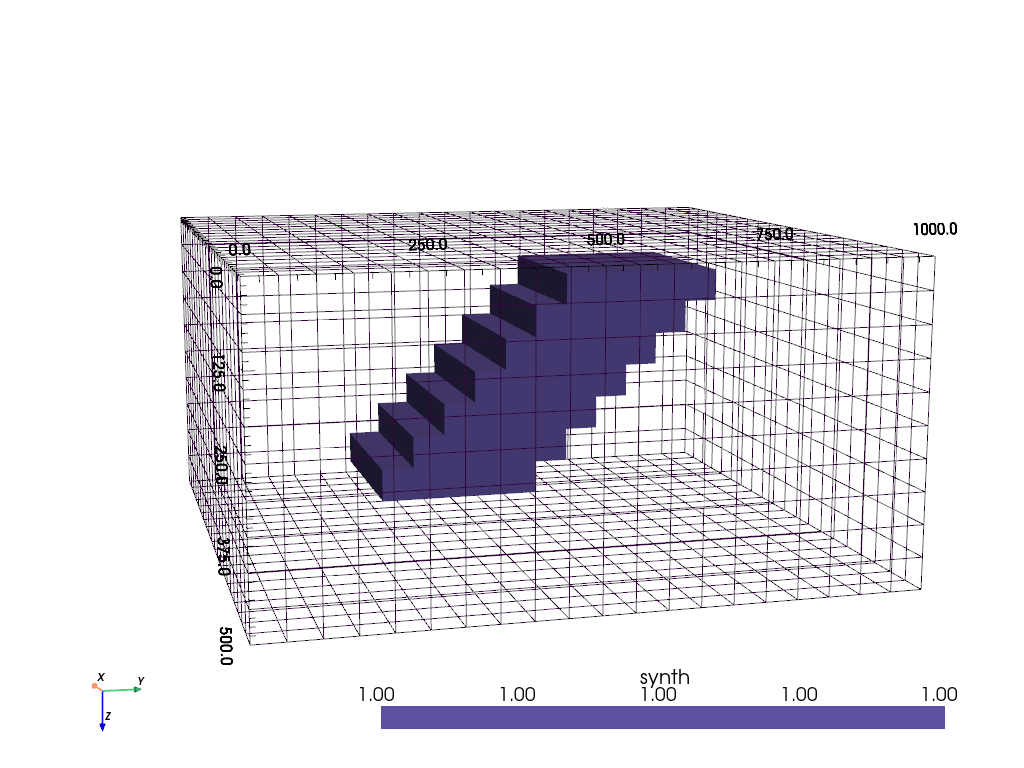
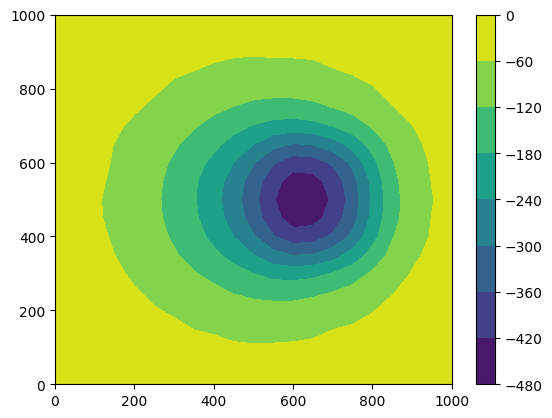
We simulate the synthetic model and display the model response.

xx, yy = np.meshgrid(x, y)
points = np.column_stack((xx.ravel(), yy.ravel(), -np.ones(np.prod(xx.shape))))
fop = GravityModelling(grid, points)
data = fop.response(grid["synth"])
noise_level = 1
data += np.random.randn(len(data)) * noise_level
plt.contourf(yy, xx, np.reshape(data, xx.shape))
plt.colorbar();

Depth weighting#

In the paper of Li & Oldenburg (1996), they propose a depth weighting of the constraints with the formula

(1)#\[\begin{align}w_z = \frac{1}{(z+z_0)^{\beta/2}}\end{align}\]
# depth weighting
bz = np.array([b.center().z() for b in grid.boundaries() if not b.outside()])
bn = np.array([b.norm().z() for b in grid.boundaries() if not b.outside()])
z0 = 50
beta = 2.0
wz = (z0 / (bz+z0))**(beta/2)

Inversion#

The inversion is rather straightforward using the standard inversion framework :py:class:pygimli.Inversion.

inv = pg.Inversion(fop=fop, verbose=True)  # , debug=True)
inv.modelTrans = pg.trans.TransCotLU(-2, 2)
# inv.setRegularization(correlationLengths=[500, 500, 100])
inv.setConstraintWeights(wz)
invmodel = inv.run(data, absoluteError=noise_level, lam=1e4,  # zWeight=0.3,
                   startModel=0.1, verbose=True)
grid["inv"] = invmodel

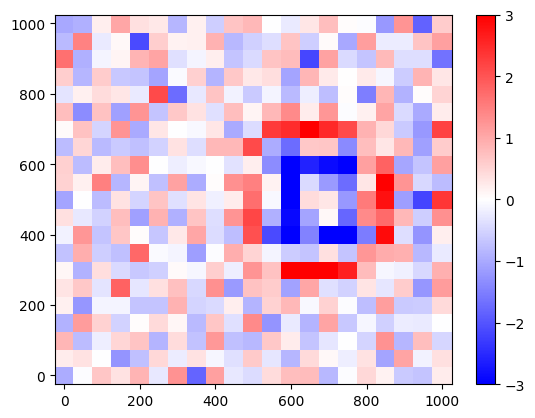
Model response

misfit = np.reshape(data-inv.response, xx.shape) / noise_level
plt.pcolor(yy, xx, misfit, cmap="bwr", vmin=-3, vmax=3)
plt.colorbar();

Visualization#

For showing the model, we again use the threshold filter with a value of 0.02. For comparison with the synthetic model, we plot the latter as a wireframe.

ftr = dict(value=0.5, scalars="synth")
pl, _ = pg.show(grid, label="synth", style="wireframe",
                filter={"threshold": ftr}, hold=True)
ftr = dict(value=0.4, scalars="inv")
pv.drawMesh(pl, grid, label="inv", style="surface", filter={"threshold": ftr},
            cMin=0, cMax=1)
pl.camera_position = "yz"
pl.camera.roll = 90
pl.camera.azimuth = 180
pl.camera.zoom(1.2)
_ = pl.show()

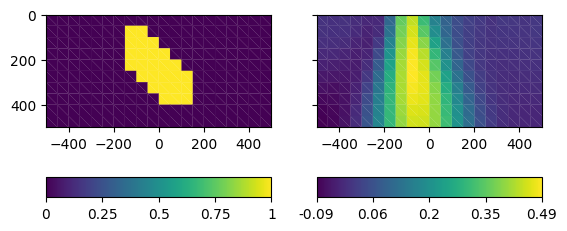
The model can outline the top part of the anomalous body and its lateral extent, but not its depth extent due to the ambiguity of gravity. We use a vertical slice to illustrate that.

slice = pg.meshtools.extract2dSlice(grid, origin=[500, 500, 0], normal=[1, 1, 0])
_, ax = plt.subplots(ncols=2, sharex=True, sharey=True)
pg.show(slice, "synth", ax=ax[0])
pg.show(slice, "inv", ax=ax[1])
ax[0].set_ylim(ax[0].get_ylim()[::-1])

References#

  • Li, Y. & Oldenburg, D. (1998): 3-D inversion of gravity data. Geophysics 63(1), 109-119.

  • Holstein, H., Sherratt, E.M., Reid, A.B.  (2007): Gravimagnetic field tensor gradiometry formulas for uniform polyhedra, SEG Ext. Abstr.